ILIAS  release_5-3 Revision v5.3.23-19-g915713cf615
Public Member Functions | Private Member Functions | Private Attributes
EigenvalueDecomposition Class Reference
+ Collaboration diagram for EigenvalueDecomposition:

Public Member Functions

 __construct ($Arg)
 Constructor: Check for symmetry, then construct the eigenvalue decomposition. More...
 
 getV ()
 Return the eigenvector matrix. More...
 
 getRealEigenvalues ()
 Return the real parts of the eigenvalues. More...
 
 getImagEigenvalues ()
 Return the imaginary parts of the eigenvalues. More...
 
 getD ()
 Return the block diagonal eigenvalue matrix. More...
 

Private Member Functions

 tred2 ()
 Symmetric Householder reduction to tridiagonal form. More...
 
 tql2 ()
 Symmetric tridiagonal QL algorithm. More...
 
 orthes ()
 Nonsymmetric reduction to Hessenberg form. More...
 
 cdiv ($xr, $xi, $yr, $yi)
 Performs complex division. More...
 
 hqr2 ()
 Nonsymmetric reduction from Hessenberg to real Schur form. More...
 

Private Attributes

 $n
 
 $issymmetric
 
 $d = array()
 
 $e = array()
 
 $V = array()
 
 $H = array()
 
 $ort
 
 $cdivr
 
 $cdivi
 

Detailed Description

Definition at line 24 of file EigenvalueDecomposition.php.

Constructor & Destructor Documentation

◆ __construct()

EigenvalueDecomposition::__construct (   $Arg)

Constructor: Check for symmetry, then construct the eigenvalue decomposition.

@access public

Parameters
ASquare matrix
Returns
Structure to access D and V.

Definition at line 782 of file EigenvalueDecomposition.php.

782 {
783 $this->A = $Arg->getArray();
784 $this->n = $Arg->getColumnDimension();
785
786 $issymmetric = true;
787 for ($j = 0; ($j < $this->n) & $issymmetric; ++$j) {
788 for ($i = 0; ($i < $this->n) & $issymmetric; ++$i) {
789 $issymmetric = ($this->A[$i][$j] == $this->A[$j][$i]);
790 }
791 }
792
793 if ($issymmetric) {
794 $this->V = $this->A;
795 // Tridiagonalize.
796 $this->tred2();
797 // Diagonalize.
798 $this->tql2();
799 } else {
800 $this->H = $this->A;
801 $this->ort = array();
802 // Reduce to Hessenberg form.
803 $this->orthes();
804 // Reduce Hessenberg to real Schur form.
805 $this->hqr2();
806 }
807 }
EigenvalueDecomposition\orthes
orthes()
Nonsymmetric reduction to Hessenberg form.
Definition: EigenvalueDecomposition.php:291
EigenvalueDecomposition\hqr2
hqr2()
Nonsymmetric reduction from Hessenberg to real Schur form.
Definition: EigenvalueDecomposition.php:398
EigenvalueDecomposition\tred2
tred2()
Symmetric Householder reduction to tridiagonal form.
Definition: EigenvalueDecomposition.php:76
EigenvalueDecomposition\tql2
tql2()
Symmetric tridiagonal QL algorithm.
Definition: EigenvalueDecomposition.php:185
$i
$i
Definition: disco.tpl.php:19

References $i, $issymmetric, $n, hqr2(), orthes(), tql2(), and tred2().

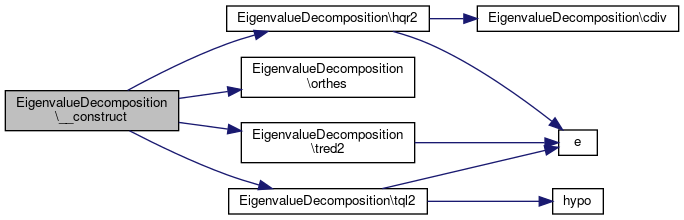
+ Here is the call graph for this function:

Member Function Documentation

◆ cdiv()

EigenvalueDecomposition::cdiv (   $xr,
  $xi,
  $yr,
  $yi 
)
private

Performs complex division.

@access private

Definition at line 373 of file EigenvalueDecomposition.php.

373 {
374 if (abs($yr) > abs($yi)) {
375 $r = $yi / $yr;
376 $d = $yr + $r * $yi;
377 $this->cdivr = ($xr + $r * $xi) / $d;
378 $this->cdivi = ($xi - $r * $xr) / $d;
379 } else {
380 $r = $yr / $yi;
381 $d = $yi + $r * $yr;
382 $this->cdivr = ($r * $xr + $xi) / $d;
383 $this->cdivi = ($r * $xi - $xr) / $d;
384 }
385 }
$r
$r
Definition: example_031.php:79

References $d, and $r.

Referenced by hqr2().

+ Here is the caller graph for this function:

◆ getD()

EigenvalueDecomposition::getD ( )

Return the block diagonal eigenvalue matrix.

@access public

Returns
D

Definition at line 849 of file EigenvalueDecomposition.php.

849 {
850 for ($i = 0; $i < $this->n; ++$i) {
851 $D[$i] = array_fill(0, $this->n, 0.0);
852 $D[$i][$i] = $this->d[$i];
853 if ($this->e[$i] == 0) {
854 continue;
855 }
856 $o = ($this->e[$i] > 0) ? $i + 1 : $i - 1;
857 $D[$i][$o] = $this->e[$i];
858 }
859 return new Matrix($D);
860 }
e
e($cmd)
Definition: flush.php:14

References $i, $n, and e().

+ Here is the call graph for this function:

◆ getImagEigenvalues()

EigenvalueDecomposition::getImagEigenvalues ( )

Return the imaginary parts of the eigenvalues.

@access public

Returns
imag(diag(D))

Definition at line 838 of file EigenvalueDecomposition.php.

838 {
839 return $this->e;
840 }

References $e.

◆ getRealEigenvalues()

EigenvalueDecomposition::getRealEigenvalues ( )

Return the real parts of the eigenvalues.

@access public

Returns
real(diag(D))

Definition at line 827 of file EigenvalueDecomposition.php.

827 {
828 return $this->d;
829 }

References $d.

◆ getV()

EigenvalueDecomposition::getV ( )

Return the eigenvector matrix.

@access public

Returns
V

Definition at line 816 of file EigenvalueDecomposition.php.

816 {
817 return new Matrix($this->V, $this->n, $this->n);
818 }

◆ hqr2()

EigenvalueDecomposition::hqr2 ( )
private

Nonsymmetric reduction from Hessenberg to real Schur form.

Code is derived from the Algol procedure hqr2, by Martin and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutine in EISPACK.

@access private

Definition at line 398 of file EigenvalueDecomposition.php.

398 {
399 // Initialize
400 $nn = $this->n;
401 $n = $nn - 1;
402 $low = 0;
403 $high = $nn - 1;
404 $eps = pow(2.0, -52.0);
405 $exshift = 0.0;
406 $p = $q = $r = $s = $z = 0;
407 // Store roots isolated by balanc and compute matrix norm
408 $norm = 0.0;
409
410 for ($i = 0; $i < $nn; ++$i) {
411 if (($i < $low) OR ($i > $high)) {
412 $this->d[$i] = $this->H[$i][$i];
413 $this->e[$i] = 0.0;
414 }
415 for ($j = max($i-1, 0); $j < $nn; ++$j) {
416 $norm = $norm + abs($this->H[$i][$j]);
417 }
418 }
419
420 // Outer loop over eigenvalue index
421 $iter = 0;
422 while ($n >= $low) {
423 // Look for single small sub-diagonal element
424 $l = $n;
425 while ($l > $low) {
426 $s = abs($this->H[$l-1][$l-1]) + abs($this->H[$l][$l]);
427 if ($s == 0.0) {
428 $s = $norm;
429 }
430 if (abs($this->H[$l][$l-1]) < $eps * $s) {
431 break;
432 }
433 --$l;
434 }
435 // Check for convergence
436 // One root found
437 if ($l == $n) {
438 $this->H[$n][$n] = $this->H[$n][$n] + $exshift;
439 $this->d[$n] = $this->H[$n][$n];
440 $this->e[$n] = 0.0;
441 --$n;
442 $iter = 0;
443 // Two roots found
444 } else if ($l == $n-1) {
445 $w = $this->H[$n][$n-1] * $this->H[$n-1][$n];
446 $p = ($this->H[$n-1][$n-1] - $this->H[$n][$n]) / 2.0;
447 $q = $p * $p + $w;
448 $z = sqrt(abs($q));
449 $this->H[$n][$n] = $this->H[$n][$n] + $exshift;
450 $this->H[$n-1][$n-1] = $this->H[$n-1][$n-1] + $exshift;
451 $x = $this->H[$n][$n];
452 // Real pair
453 if ($q >= 0) {
454 if ($p >= 0) {
455 $z = $p + $z;
456 } else {
457 $z = $p - $z;
458 }
459 $this->d[$n-1] = $x + $z;
460 $this->d[$n] = $this->d[$n-1];
461 if ($z != 0.0) {
462 $this->d[$n] = $x - $w / $z;
463 }
464 $this->e[$n-1] = 0.0;
465 $this->e[$n] = 0.0;
466 $x = $this->H[$n][$n-1];
467 $s = abs($x) + abs($z);
468 $p = $x / $s;
469 $q = $z / $s;
470 $r = sqrt($p * $p + $q * $q);
471 $p = $p / $r;
472 $q = $q / $r;
473 // Row modification
474 for ($j = $n-1; $j < $nn; ++$j) {
475 $z = $this->H[$n-1][$j];
476 $this->H[$n-1][$j] = $q * $z + $p * $this->H[$n][$j];
477 $this->H[$n][$j] = $q * $this->H[$n][$j] - $p * $z;
478 }
479 // Column modification
480 for ($i = 0; $i <= n; ++$i) {
481 $z = $this->H[$i][$n-1];
482 $this->H[$i][$n-1] = $q * $z + $p * $this->H[$i][$n];
483 $this->H[$i][$n] = $q * $this->H[$i][$n] - $p * $z;
484 }
485 // Accumulate transformations
486 for ($i = $low; $i <= $high; ++$i) {
487 $z = $this->V[$i][$n-1];
488 $this->V[$i][$n-1] = $q * $z + $p * $this->V[$i][$n];
489 $this->V[$i][$n] = $q * $this->V[$i][$n] - $p * $z;
490 }
491 // Complex pair
492 } else {
493 $this->d[$n-1] = $x + $p;
494 $this->d[$n] = $x + $p;
495 $this->e[$n-1] = $z;
496 $this->e[$n] = -$z;
497 }
498 $n = $n - 2;
499 $iter = 0;
500 // No convergence yet
501 } else {
502 // Form shift
503 $x = $this->H[$n][$n];
504 $y = 0.0;
505 $w = 0.0;
506 if ($l < $n) {
507 $y = $this->H[$n-1][$n-1];
508 $w = $this->H[$n][$n-1] * $this->H[$n-1][$n];
509 }
510 // Wilkinson's original ad hoc shift
511 if ($iter == 10) {
512 $exshift += $x;
513 for ($i = $low; $i <= $n; ++$i) {
514 $this->H[$i][$i] -= $x;
515 }
516 $s = abs($this->H[$n][$n-1]) + abs($this->H[$n-1][$n-2]);
517 $x = $y = 0.75 * $s;
518 $w = -0.4375 * $s * $s;
519 }
520 // MATLAB's new ad hoc shift
521 if ($iter == 30) {
522 $s = ($y - $x) / 2.0;
523 $s = $s * $s + $w;
524 if ($s > 0) {
525 $s = sqrt($s);
526 if ($y < $x) {
527 $s = -$s;
528 }
529 $s = $x - $w / (($y - $x) / 2.0 + $s);
530 for ($i = $low; $i <= $n; ++$i) {
531 $this->H[$i][$i] -= $s;
532 }
533 $exshift += $s;
534 $x = $y = $w = 0.964;
535 }
536 }
537 // Could check iteration count here.
538 $iter = $iter + 1;
539 // Look for two consecutive small sub-diagonal elements
540 $m = $n - 2;
541 while ($m >= $l) {
542 $z = $this->H[$m][$m];
543 $r = $x - $z;
544 $s = $y - $z;
545 $p = ($r * $s - $w) / $this->H[$m+1][$m] + $this->H[$m][$m+1];
546 $q = $this->H[$m+1][$m+1] - $z - $r - $s;
547 $r = $this->H[$m+2][$m+1];
548 $s = abs($p) + abs($q) + abs($r);
549 $p = $p / $s;
550 $q = $q / $s;
551 $r = $r / $s;
552 if ($m == $l) {
553 break;
554 }
555 if (abs($this->H[$m][$m-1]) * (abs($q) + abs($r)) <
556 $eps * (abs($p) * (abs($this->H[$m-1][$m-1]) + abs($z) + abs($this->H[$m+1][$m+1])))) {
557 break;
558 }
559 --$m;
560 }
561 for ($i = $m + 2; $i <= $n; ++$i) {
562 $this->H[$i][$i-2] = 0.0;
563 if ($i > $m+2) {
564 $this->H[$i][$i-3] = 0.0;
565 }
566 }
567 // Double QR step involving rows l:n and columns m:n
568 for ($k = $m; $k <= $n-1; ++$k) {
569 $notlast = ($k != $n-1);
570 if ($k != $m) {
571 $p = $this->H[$k][$k-1];
572 $q = $this->H[$k+1][$k-1];
573 $r = ($notlast ? $this->H[$k+2][$k-1] : 0.0);
574 $x = abs($p) + abs($q) + abs($r);
575 if ($x != 0.0) {
576 $p = $p / $x;
577 $q = $q / $x;
578 $r = $r / $x;
579 }
580 }
581 if ($x == 0.0) {
582 break;
583 }
584 $s = sqrt($p * $p + $q * $q + $r * $r);
585 if ($p < 0) {
586 $s = -$s;
587 }
588 if ($s != 0) {
589 if ($k != $m) {
590 $this->H[$k][$k-1] = -$s * $x;
591 } elseif ($l != $m) {
592 $this->H[$k][$k-1] = -$this->H[$k][$k-1];
593 }
594 $p = $p + $s;
595 $x = $p / $s;
596 $y = $q / $s;
597 $z = $r / $s;
598 $q = $q / $p;
599 $r = $r / $p;
600 // Row modification
601 for ($j = $k; $j < $nn; ++$j) {
602 $p = $this->H[$k][$j] + $q * $this->H[$k+1][$j];
603 if ($notlast) {
604 $p = $p + $r * $this->H[$k+2][$j];
605 $this->H[$k+2][$j] = $this->H[$k+2][$j] - $p * $z;
606 }
607 $this->H[$k][$j] = $this->H[$k][$j] - $p * $x;
608 $this->H[$k+1][$j] = $this->H[$k+1][$j] - $p * $y;
609 }
610 // Column modification
611 for ($i = 0; $i <= min($n, $k+3); ++$i) {
612 $p = $x * $this->H[$i][$k] + $y * $this->H[$i][$k+1];
613 if ($notlast) {
614 $p = $p + $z * $this->H[$i][$k+2];
615 $this->H[$i][$k+2] = $this->H[$i][$k+2] - $p * $r;
616 }
617 $this->H[$i][$k] = $this->H[$i][$k] - $p;
618 $this->H[$i][$k+1] = $this->H[$i][$k+1] - $p * $q;
619 }
620 // Accumulate transformations
621 for ($i = $low; $i <= $high; ++$i) {
622 $p = $x * $this->V[$i][$k] + $y * $this->V[$i][$k+1];
623 if ($notlast) {
624 $p = $p + $z * $this->V[$i][$k+2];
625 $this->V[$i][$k+2] = $this->V[$i][$k+2] - $p * $r;
626 }
627 $this->V[$i][$k] = $this->V[$i][$k] - $p;
628 $this->V[$i][$k+1] = $this->V[$i][$k+1] - $p * $q;
629 }
630 } // ($s != 0)
631 } // k loop
632 } // check convergence
633 } // while ($n >= $low)
634
635 // Backsubstitute to find vectors of upper triangular form
636 if ($norm == 0.0) {
637 return;
638 }
639
640 for ($n = $nn-1; $n >= 0; --$n) {
641 $p = $this->d[$n];
642 $q = $this->e[$n];
643 // Real vector
644 if ($q == 0) {
645 $l = $n;
646 $this->H[$n][$n] = 1.0;
647 for ($i = $n-1; $i >= 0; --$i) {
648 $w = $this->H[$i][$i] - $p;
649 $r = 0.0;
650 for ($j = $l; $j <= $n; ++$j) {
651 $r = $r + $this->H[$i][$j] * $this->H[$j][$n];
652 }
653 if ($this->e[$i] < 0.0) {
654 $z = $w;
655 $s = $r;
656 } else {
657 $l = $i;
658 if ($this->e[$i] == 0.0) {
659 if ($w != 0.0) {
660 $this->H[$i][$n] = -$r / $w;
661 } else {
662 $this->H[$i][$n] = -$r / ($eps * $norm);
663 }
664 // Solve real equations
665 } else {
666 $x = $this->H[$i][$i+1];
667 $y = $this->H[$i+1][$i];
668 $q = ($this->d[$i] - $p) * ($this->d[$i] - $p) + $this->e[$i] * $this->e[$i];
669 $t = ($x * $s - $z * $r) / $q;
670 $this->H[$i][$n] = $t;
671 if (abs($x) > abs($z)) {
672 $this->H[$i+1][$n] = (-$r - $w * $t) / $x;
673 } else {
674 $this->H[$i+1][$n] = (-$s - $y * $t) / $z;
675 }
676 }
677 // Overflow control
678 $t = abs($this->H[$i][$n]);
679 if (($eps * $t) * $t > 1) {
680 for ($j = $i; $j <= $n; ++$j) {
681 $this->H[$j][$n] = $this->H[$j][$n] / $t;
682 }
683 }
684 }
685 }
686 // Complex vector
687 } else if ($q < 0) {
688 $l = $n-1;
689 // Last vector component imaginary so matrix is triangular
690 if (abs($this->H[$n][$n-1]) > abs($this->H[$n-1][$n])) {
691 $this->H[$n-1][$n-1] = $q / $this->H[$n][$n-1];
692 $this->H[$n-1][$n] = -($this->H[$n][$n] - $p) / $this->H[$n][$n-1];
693 } else {
694 $this->cdiv(0.0, -$this->H[$n-1][$n], $this->H[$n-1][$n-1] - $p, $q);
695 $this->H[$n-1][$n-1] = $this->cdivr;
696 $this->H[$n-1][$n] = $this->cdivi;
697 }
698 $this->H[$n][$n-1] = 0.0;
699 $this->H[$n][$n] = 1.0;
700 for ($i = $n-2; $i >= 0; --$i) {
701 // double ra,sa,vr,vi;
702 $ra = 0.0;
703 $sa = 0.0;
704 for ($j = $l; $j <= $n; ++$j) {
705 $ra = $ra + $this->H[$i][$j] * $this->H[$j][$n-1];
706 $sa = $sa + $this->H[$i][$j] * $this->H[$j][$n];
707 }
708 $w = $this->H[$i][$i] - $p;
709 if ($this->e[$i] < 0.0) {
710 $z = $w;
711 $r = $ra;
712 $s = $sa;
713 } else {
714 $l = $i;
715 if ($this->e[$i] == 0) {
716 $this->cdiv(-$ra, -$sa, $w, $q);
717 $this->H[$i][$n-1] = $this->cdivr;
718 $this->H[$i][$n] = $this->cdivi;
719 } else {
720 // Solve complex equations
721 $x = $this->H[$i][$i+1];
722 $y = $this->H[$i+1][$i];
723 $vr = ($this->d[$i] - $p) * ($this->d[$i] - $p) + $this->e[$i] * $this->e[$i] - $q * $q;
724 $vi = ($this->d[$i] - $p) * 2.0 * $q;
725 if ($vr == 0.0 & $vi == 0.0) {
726 $vr = $eps * $norm * (abs($w) + abs($q) + abs($x) + abs($y) + abs($z));
727 }
728 $this->cdiv($x * $r - $z * $ra + $q * $sa, $x * $s - $z * $sa - $q * $ra, $vr, $vi);
729 $this->H[$i][$n-1] = $this->cdivr;
730 $this->H[$i][$n] = $this->cdivi;
731 if (abs($x) > (abs($z) + abs($q))) {
732 $this->H[$i+1][$n-1] = (-$ra - $w * $this->H[$i][$n-1] + $q * $this->H[$i][$n]) / $x;
733 $this->H[$i+1][$n] = (-$sa - $w * $this->H[$i][$n] - $q * $this->H[$i][$n-1]) / $x;
734 } else {
735 $this->cdiv(-$r - $y * $this->H[$i][$n-1], -$s - $y * $this->H[$i][$n], $z, $q);
736 $this->H[$i+1][$n-1] = $this->cdivr;
737 $this->H[$i+1][$n] = $this->cdivi;
738 }
739 }
740 // Overflow control
741 $t = max(abs($this->H[$i][$n-1]),abs($this->H[$i][$n]));
742 if (($eps * $t) * $t > 1) {
743 for ($j = $i; $j <= $n; ++$j) {
744 $this->H[$j][$n-1] = $this->H[$j][$n-1] / $t;
745 $this->H[$j][$n] = $this->H[$j][$n] / $t;
746 }
747 }
748 } // end else
749 } // end for
750 } // end else for complex case
751 } // end for
752
753 // Vectors of isolated roots
754 for ($i = 0; $i < $nn; ++$i) {
755 if ($i < $low | $i > $high) {
756 for ($j = $i; $j < $nn; ++$j) {
757 $this->V[$i][$j] = $this->H[$i][$j];
758 }
759 }
760 }
761
762 // Back transformation to get eigenvectors of original matrix
763 for ($j = $nn-1; $j >= $low; --$j) {
764 for ($i = $low; $i <= $high; ++$i) {
765 $z = 0.0;
766 for ($k = $low; $k <= min($j,$high); ++$k) {
767 $z = $z + $this->V[$i][$k] * $this->H[$k][$j];
768 }
769 $this->V[$i][$j] = $z;
770 }
771 }
772 } // end hqr2
$l
global $l
Definition: afr.php:30
EigenvalueDecomposition\cdiv
cdiv($xr, $xi, $yr, $yi)
Performs complex division.
Definition: EigenvalueDecomposition.php:373
$y
$y
Definition: example_007.php:83
$x
$x
Definition: example_009.php:98
$w
$w
Definition: example_009.php:100
$eps
$eps
Definition: metadata.php:61
$s
$s
Definition: pwgen.php:45
$m
$m
Definition: show_metadata.php:25

References $cdivi, $cdivr, $eps, $i, $l, $m, $n, $r, $s, $t, $w, $x, $y, cdiv(), and e().

Referenced by __construct().

+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ orthes()

EigenvalueDecomposition::orthes ( )
private

Nonsymmetric reduction to Hessenberg form.

This is derived from the Algol procedures orthes and ortran, by Martin and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutines in EISPACK.

@access private

Definition at line 291 of file EigenvalueDecomposition.php.

291 {
292 $low = 0;
293 $high = $this->n-1;
294
295 for ($m = $low+1; $m <= $high-1; ++$m) {
296 // Scale column.
297 $scale = 0.0;
298 for ($i = $m; $i <= $high; ++$i) {
299 $scale = $scale + abs($this->H[$i][$m-1]);
300 }
301 if ($scale != 0.0) {
302 // Compute Householder transformation.
303 $h = 0.0;
304 for ($i = $high; $i >= $m; --$i) {
305 $this->ort[$i] = $this->H[$i][$m-1] / $scale;
306 $h += $this->ort[$i] * $this->ort[$i];
307 }
308 $g = sqrt($h);
309 if ($this->ort[$m] > 0) {
310 $g *= -1;
311 }
312 $h -= $this->ort[$m] * $g;
313 $this->ort[$m] -= $g;
314 // Apply Householder similarity transformation
315 // H = (I -u * u' / h) * H * (I -u * u') / h)
316 for ($j = $m; $j < $this->n; ++$j) {
317 $f = 0.0;
318 for ($i = $high; $i >= $m; --$i) {
319 $f += $this->ort[$i] * $this->H[$i][$j];
320 }
321 $f /= $h;
322 for ($i = $m; $i <= $high; ++$i) {
323 $this->H[$i][$j] -= $f * $this->ort[$i];
324 }
325 }
326 for ($i = 0; $i <= $high; ++$i) {
327 $f = 0.0;
328 for ($j = $high; $j >= $m; --$j) {
329 $f += $this->ort[$j] * $this->H[$i][$j];
330 }
331 $f = $f / $h;
332 for ($j = $m; $j <= $high; ++$j) {
333 $this->H[$i][$j] -= $f * $this->ort[$j];
334 }
335 }
336 $this->ort[$m] = $scale * $this->ort[$m];
337 $this->H[$m][$m-1] = $scale * $g;
338 }
339 }
340
341 // Accumulate transformations (Algol's ortran).
342 for ($i = 0; $i < $this->n; ++$i) {
343 for ($j = 0; $j < $this->n; ++$j) {
344 $this->V[$i][$j] = ($i == $j ? 1.0 : 0.0);
345 }
346 }
347 for ($m = $high-1; $m >= $low+1; --$m) {
348 if ($this->H[$m][$m-1] != 0.0) {
349 for ($i = $m+1; $i <= $high; ++$i) {
350 $this->ort[$i] = $this->H[$i][$m-1];
351 }
352 for ($j = $m; $j <= $high; ++$j) {
353 $g = 0.0;
354 for ($i = $m; $i <= $high; ++$i) {
355 $g += $this->ort[$i] * $this->V[$i][$j];
356 }
357 // Double division avoids possible underflow
358 $g = ($g / $this->ort[$m]) / $this->H[$m][$m-1];
359 for ($i = $m; $i <= $high; ++$i) {
360 $this->V[$i][$j] += $g * $this->ort[$i];
361 }
362 }
363 }
364 }
365 }
$h
$h
Definition: example_009.php:101

References $h, $i, $m, and $n.

Referenced by __construct().

+ Here is the caller graph for this function:

◆ tql2()

EigenvalueDecomposition::tql2 ( )
private

Symmetric tridiagonal QL algorithm.

This is derived from the Algol procedures tql2, by Bowdler, Martin, Reinsch, and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutine in EISPACK.

@access private

Definition at line 185 of file EigenvalueDecomposition.php.

185 {
186 for ($i = 1; $i < $this->n; ++$i) {
187 $this->e[$i-1] = $this->e[$i];
188 }
189 $this->e[$this->n-1] = 0.0;
190 $f = 0.0;
191 $tst1 = 0.0;
192 $eps = pow(2.0,-52.0);
193
194 for ($l = 0; $l < $this->n; ++$l) {
195 // Find small subdiagonal element
196 $tst1 = max($tst1, abs($this->d[$l]) + abs($this->e[$l]));
197 $m = $l;
198 while ($m < $this->n) {
199 if (abs($this->e[$m]) <= $eps * $tst1)
200 break;
201 ++$m;
202 }
203 // If m == l, $this->d[l] is an eigenvalue,
204 // otherwise, iterate.
205 if ($m > $l) {
206 $iter = 0;
207 do {
208 // Could check iteration count here.
209 $iter += 1;
210 // Compute implicit shift
211 $g = $this->d[$l];
212 $p = ($this->d[$l+1] - $g) / (2.0 * $this->e[$l]);
213 $r = hypo($p, 1.0);
214 if ($p < 0)
215 $r *= -1;
216 $this->d[$l] = $this->e[$l] / ($p + $r);
217 $this->d[$l+1] = $this->e[$l] * ($p + $r);
218 $dl1 = $this->d[$l+1];
219 $h = $g - $this->d[$l];
220 for ($i = $l + 2; $i < $this->n; ++$i)
221 $this->d[$i] -= $h;
222 $f += $h;
223 // Implicit QL transformation.
224 $p = $this->d[$m];
225 $c = 1.0;
226 $c2 = $c3 = $c;
227 $el1 = $this->e[$l + 1];
228 $s = $s2 = 0.0;
229 for ($i = $m-1; $i >= $l; --$i) {
230 $c3 = $c2;
231 $c2 = $c;
232 $s2 = $s;
233 $g = $c * $this->e[$i];
234 $h = $c * $p;
235 $r = hypo($p, $this->e[$i]);
236 $this->e[$i+1] = $s * $r;
237 $s = $this->e[$i] / $r;
238 $c = $p / $r;
239 $p = $c * $this->d[$i] - $s * $g;
240 $this->d[$i+1] = $h + $s * ($c * $g + $s * $this->d[$i]);
241 // Accumulate transformation.
242 for ($k = 0; $k < $this->n; ++$k) {
243 $h = $this->V[$k][$i+1];
244 $this->V[$k][$i+1] = $s * $this->V[$k][$i] + $c * $h;
245 $this->V[$k][$i] = $c * $this->V[$k][$i] - $s * $h;
246 }
247 }
248 $p = -$s * $s2 * $c3 * $el1 * $this->e[$l] / $dl1;
249 $this->e[$l] = $s * $p;
250 $this->d[$l] = $c * $p;
251 // Check for convergence.
252 } while (abs($this->e[$l]) > $eps * $tst1);
253 }
254 $this->d[$l] = $this->d[$l] + $f;
255 $this->e[$l] = 0.0;
256 }
257
258 // Sort eigenvalues and corresponding vectors.
259 for ($i = 0; $i < $this->n - 1; ++$i) {
260 $k = $i;
261 $p = $this->d[$i];
262 for ($j = $i+1; $j < $this->n; ++$j) {
263 if ($this->d[$j] < $p) {
264 $k = $j;
265 $p = $this->d[$j];
266 }
267 }
268 if ($k != $i) {
269 $this->d[$k] = $this->d[$i];
270 $this->d[$i] = $p;
271 for ($j = 0; $j < $this->n; ++$j) {
272 $p = $this->V[$j][$i];
273 $this->V[$j][$i] = $this->V[$j][$k];
274 $this->V[$j][$k] = $p;
275 }
276 }
277 }
278 }
hypo
hypo($a, $b)
Definition: Maths.php:14

References $eps, $h, $i, $l, $m, $n, $r, $s, e(), and hypo().

Referenced by __construct().

+ Here is the call graph for this function:
+ Here is the caller graph for this function:

◆ tred2()

EigenvalueDecomposition::tred2 ( )
private

Symmetric Householder reduction to tridiagonal form.

@access private

Definition at line 76 of file EigenvalueDecomposition.php.

76 {
77 // This is derived from the Algol procedures tred2 by
78 // Bowdler, Martin, Reinsch, and Wilkinson, Handbook for
79 // Auto. Comp., Vol.ii-Linear Algebra, and the corresponding
80 // Fortran subroutine in EISPACK.
81 $this->d = $this->V[$this->n-1];
82 // Householder reduction to tridiagonal form.
83 for ($i = $this->n-1; $i > 0; --$i) {
84 $i_ = $i -1;
85 // Scale to avoid under/overflow.
86 $h = $scale = 0.0;
87 $scale += array_sum(array_map(abs, $this->d));
88 if ($scale == 0.0) {
89 $this->e[$i] = $this->d[$i_];
90 $this->d = array_slice($this->V[$i_], 0, $i_);
91 for ($j = 0; $j < $i; ++$j) {
92 $this->V[$j][$i] = $this->V[$i][$j] = 0.0;
93 }
94 } else {
95 // Generate Householder vector.
96 for ($k = 0; $k < $i; ++$k) {
97 $this->d[$k] /= $scale;
98 $h += pow($this->d[$k], 2);
99 }
100 $f = $this->d[$i_];
101 $g = sqrt($h);
102 if ($f > 0) {
103 $g = -$g;
104 }
105 $this->e[$i] = $scale * $g;
106 $h = $h - $f * $g;
107 $this->d[$i_] = $f - $g;
108 for ($j = 0; $j < $i; ++$j) {
109 $this->e[$j] = 0.0;
110 }
111 // Apply similarity transformation to remaining columns.
112 for ($j = 0; $j < $i; ++$j) {
113 $f = $this->d[$j];
114 $this->V[$j][$i] = $f;
115 $g = $this->e[$j] + $this->V[$j][$j] * $f;
116 for ($k = $j+1; $k <= $i_; ++$k) {
117 $g += $this->V[$k][$j] * $this->d[$k];
118 $this->e[$k] += $this->V[$k][$j] * $f;
119 }
120 $this->e[$j] = $g;
121 }
122 $f = 0.0;
123 for ($j = 0; $j < $i; ++$j) {
124 $this->e[$j] /= $h;
125 $f += $this->e[$j] * $this->d[$j];
126 }
127 $hh = $f / (2 * $h);
128 for ($j=0; $j < $i; ++$j) {
129 $this->e[$j] -= $hh * $this->d[$j];
130 }
131 for ($j = 0; $j < $i; ++$j) {
132 $f = $this->d[$j];
133 $g = $this->e[$j];
134 for ($k = $j; $k <= $i_; ++$k) {
135 $this->V[$k][$j] -= ($f * $this->e[$k] + $g * $this->d[$k]);
136 }
137 $this->d[$j] = $this->V[$i-1][$j];
138 $this->V[$i][$j] = 0.0;
139 }
140 }
141 $this->d[$i] = $h;
142 }
143
144 // Accumulate transformations.
145 for ($i = 0; $i < $this->n-1; ++$i) {
146 $this->V[$this->n-1][$i] = $this->V[$i][$i];
147 $this->V[$i][$i] = 1.0;
148 $h = $this->d[$i+1];
149 if ($h != 0.0) {
150 for ($k = 0; $k <= $i; ++$k) {
151 $this->d[$k] = $this->V[$k][$i+1] / $h;
152 }
153 for ($j = 0; $j <= $i; ++$j) {
154 $g = 0.0;
155 for ($k = 0; $k <= $i; ++$k) {
156 $g += $this->V[$k][$i+1] * $this->V[$k][$j];
157 }
158 for ($k = 0; $k <= $i; ++$k) {
159 $this->V[$k][$j] -= $g * $this->d[$k];
160 }
161 }
162 }
163 for ($k = 0; $k <= $i; ++$k) {
164 $this->V[$k][$i+1] = 0.0;
165 }
166 }
167
168 $this->d = $this->V[$this->n-1];
169 $this->V[$this->n-1] = array_fill(0, $j, 0.0);
170 $this->V[$this->n-1][$this->n-1] = 1.0;
171 $this->e[0] = 0.0;
172 }

References $h, $i, and e().

Referenced by __construct().

+ Here is the call graph for this function:
+ Here is the caller graph for this function:

Field Documentation

◆ $cdivi

EigenvalueDecomposition::$cdivi
private

Definition at line 68 of file EigenvalueDecomposition.php.

Referenced by hqr2().

◆ $cdivr

EigenvalueDecomposition::$cdivr
private

Definition at line 67 of file EigenvalueDecomposition.php.

Referenced by hqr2().

◆ $d

EigenvalueDecomposition::$d = array()
private

Definition at line 42 of file EigenvalueDecomposition.php.

Referenced by cdiv(), and getRealEigenvalues().

◆ $e

EigenvalueDecomposition::$e = array()
private

Definition at line 43 of file EigenvalueDecomposition.php.

Referenced by getImagEigenvalues().

◆ $H

EigenvalueDecomposition::$H = array()
private

Definition at line 55 of file EigenvalueDecomposition.php.

◆ $issymmetric

EigenvalueDecomposition::$issymmetric
private

Definition at line 36 of file EigenvalueDecomposition.php.

Referenced by __construct().

◆ $n

EigenvalueDecomposition::$n
private

Definition at line 30 of file EigenvalueDecomposition.php.

Referenced by __construct(), getD(), hqr2(), orthes(), and tql2().

◆ $ort

EigenvalueDecomposition::$ort
private

Definition at line 61 of file EigenvalueDecomposition.php.

◆ $V

EigenvalueDecomposition::$V = array()
private

Definition at line 49 of file EigenvalueDecomposition.php.

The documentation for this class was generated from the following file: