Collaboration diagram for PHPExcel_Calculation_Engineering:
Collaboration diagram for PHPExcel_Calculation_Engineering:Static Public Member Functions | |
| static | _parseComplex ($complexNumber) |
| _parseComplex More... | |
| static | BESSELI ($x, $ord) |
| static | BESSELJ ($x, $ord) |
| static | BESSELK ($x, $ord) |
| static | BESSELY ($x, $ord) |
| static | BINTODEC ($x) |
| static | BINTOHEX ($x, $places=NULL) |
| static | BINTOOCT ($x, $places=NULL) |
| static | DECTOBIN ($x, $places=NULL) |
| static | DECTOHEX ($x, $places=null) |
| static | DECTOOCT ($x, $places=null) |
| static | HEXTOBIN ($x, $places=null) |
| static | HEXTODEC ($x) |
| static | HEXTOOCT ($x, $places=null) |
| static | OCTTOBIN ($x, $places=null) |
| static | OCTTODEC ($x) |
| static | OCTTOHEX ($x, $places=null) |
| static | COMPLEX ($realNumber=0.0, $imaginary=0.0, $suffix='i') |
| static | IMAGINARY ($complexNumber) |
| static | IMREAL ($complexNumber) |
| static | IMABS ($complexNumber) |
| IMABS. More... | |
| static | IMARGUMENT ($complexNumber) |
| IMARGUMENT. More... | |
| static | IMCONJUGATE ($complexNumber) |
| IMCONJUGATE. More... | |
| static | IMCOS ($complexNumber) |
| IMCOS. More... | |
| static | IMSIN ($complexNumber) |
| IMSIN. More... | |
| static | IMSQRT ($complexNumber) |
| IMSQRT. More... | |
| static | IMLN ($complexNumber) |
| IMLN. More... | |
| static | IMLOG10 ($complexNumber) |
| IMLOG10. More... | |
| static | IMLOG2 ($complexNumber) |
| IMLOG2. More... | |
| static | IMEXP ($complexNumber) |
| IMEXP. More... | |
| static | IMPOWER ($complexNumber, $realNumber) |
| IMPOWER. More... | |
| static | IMDIV ($complexDividend, $complexDivisor) |
| IMDIV. More... | |
| static | IMSUB ($complexNumber1, $complexNumber2) |
| IMSUB. More... | |
| static | IMSUM () |
| IMSUM. More... | |
| static | IMPRODUCT () |
| IMPRODUCT. More... | |
| static | DELTA ($a, $b=0) |
| DELTA. More... | |
| static | GESTEP ($number, $step=0) |
| GESTEP. More... | |
| static | _erfVal ($x) |
| static | ERF ($lower, $upper=NULL) |
| ERF. More... | |
| static | ERFC ($x) |
| ERFC. More... | |
| static | getConversionGroups () |
| getConversionGroups Returns a list of the different conversion groups for UOM conversions More... | |
| static | getConversionGroupUnits ($group=NULL) |
| getConversionGroupUnits Returns an array of units of measure, for a specified conversion group, or for all groups More... | |
| static | getConversionGroupUnitDetails ($group=NULL) |
| getConversionGroupUnitDetails More... | |
| static | getConversionMultipliers () |
| getConversionMultipliers Returns an array of the Multiplier prefixes that can be used with Units of Measure in CONVERTUOM() More... | |
| static | CONVERTUOM ($value, $fromUOM, $toUOM) |
| CONVERTUOM. More... | |
Static Private Member Functions | |
| static | _cleanComplex ($complexNumber) |
| Cleans the leading characters in a complex number string. More... | |
| static | _nbrConversionFormat ($xVal, $places) |
| Formats a number base string value with leading zeroes. More... | |
| static | _Besselk0 ($fNum) |
| static | _Besselk1 ($fNum) |
| static | _Bessely0 ($fNum) |
| static | _Bessely1 ($fNum) |
| static | _erfcVal ($x) |
Static Private Attributes | |
| static | $_conversionUnits |
| static | $_conversionMultipliers |
| static | $_unitConversions |
| static | $_two_sqrtpi = 1.128379167095512574 |
| static | $_one_sqrtpi = 0.564189583547756287 |
Detailed Description
Definition at line 50 of file Engineering.php.
Member Function Documentation
◆ _Besselk0()
|
staticprivate |
Definition at line 884 of file Engineering.php.
Referenced by BESSELK().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ _Besselk1()
|
staticprivate |
Definition at line 901 of file Engineering.php.
Referenced by BESSELK().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ _Bessely0()
|
staticprivate |
Definition at line 966 of file Engineering.php.
Referenced by BESSELY().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
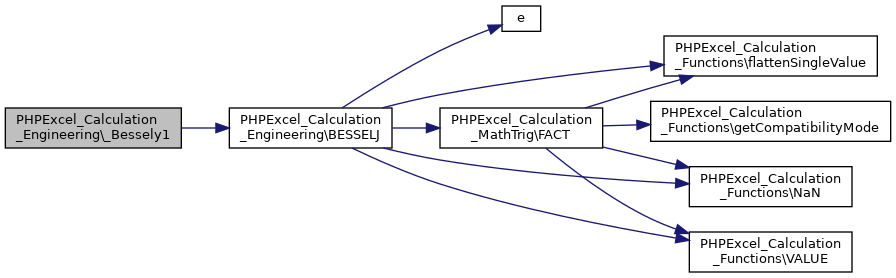
Here is the caller graph for this function:◆ _Bessely1()
|
staticprivate |
Definition at line 984 of file Engineering.php.
Referenced by BESSELY().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ _cleanComplex()
|
staticprivate |
Cleans the leading characters in a complex number string.
- Parameters
-
string $complexNumber The complex number to clean
- Returns
- string The "cleaned" complex number
Definition at line 749 of file Engineering.php.
Referenced by IMCONJUGATE(), and IMDIV().
 Here is the caller graph for this function:
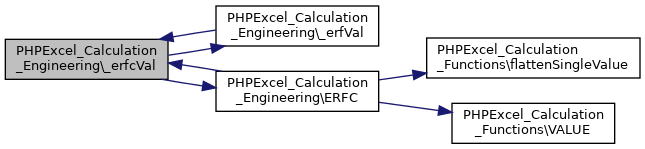
Here is the caller graph for this function:◆ _erfcVal()
|
staticprivate |
Definition at line 2289 of file Engineering.php.
References $d, $n, $t, $x, _erfVal(), ERFC(), and PRECISION.
Referenced by _erfVal(), and ERFC().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ _erfVal()
|
static |
Definition at line 2228 of file Engineering.php.
References $x, _erfcVal(), and PRECISION.
Referenced by _erfcVal(), ERF(), and PHPExcel_Calculation_Statistical\NORMDIST().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
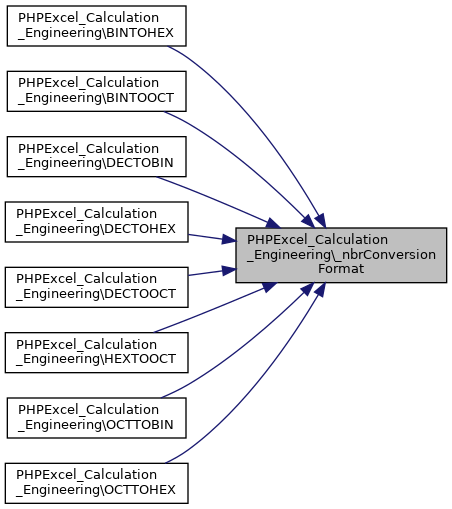
Here is the caller graph for this function:◆ _nbrConversionFormat()
|
staticprivate |
Formats a number base string value with leading zeroes.
- Parameters
-
string $xVal The "number" to pad integer $places The length that we want to pad this value
- Returns
- string The padded "number"
Definition at line 764 of file Engineering.php.
References PHPExcel_Calculation_Functions\NaN().
Referenced by BINTOHEX(), BINTOOCT(), DECTOBIN(), DECTOHEX(), DECTOOCT(), HEXTOOCT(), OCTTOBIN(), and OCTTOHEX().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
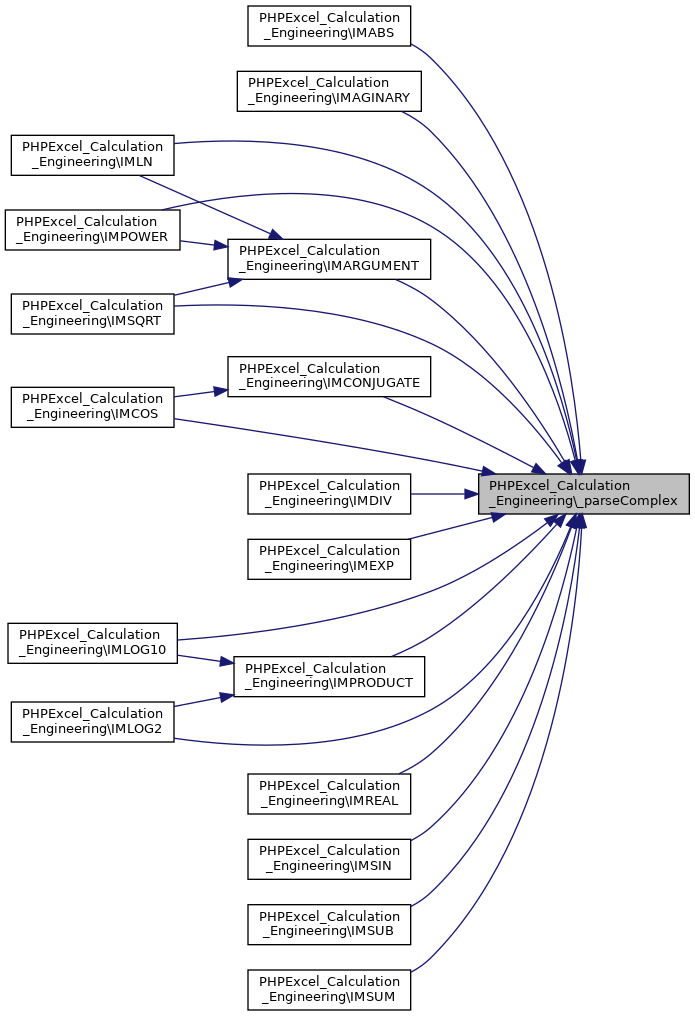
Here is the caller graph for this function:◆ _parseComplex()
|
static |
_parseComplex
Parses a complex number into its real and imaginary parts, and an I or J suffix
- Parameters
-
string $complexNumber The complex number
- Returns
- string[] Indexed on "real", "imaginary" and "suffix"
Definition at line 696 of file Engineering.php.
Referenced by IMABS(), IMAGINARY(), IMARGUMENT(), IMCONJUGATE(), IMCOS(), IMDIV(), IMEXP(), IMLN(), IMLOG10(), IMLOG2(), IMPOWER(), IMPRODUCT(), IMREAL(), IMSIN(), IMSQRT(), IMSUB(), and IMSUM().
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ BESSELI()
|
static |
Definition at line 796 of file Engineering.php.
References $x, e(), PHPExcel_Calculation_MathTrig\FACT(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
Referenced by _Besselk0(), and _Besselk1().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ BESSELJ()
|
static |
Definition at line 848 of file Engineering.php.
References $x, e(), PHPExcel_Calculation_MathTrig\FACT(), PHPExcel_Calculation_Functions\flattenSingleValue(), M_2DIVPI, PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
Referenced by _Bessely0(), and _Bessely1().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ BESSELK()
|
static |
Definition at line 937 of file Engineering.php.
References $n, $x, _Besselk0(), _Besselk1(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ BESSELY()
|
static |
Definition at line 1017 of file Engineering.php.
References $n, $x, _Bessely0(), _Bessely1(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ BINTODEC()
|
static |
Definition at line 1064 of file Engineering.php.
References $out, $x, PHPExcel_Calculation_Functions\COMPATIBILITY_GNUMERIC, PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ BINTOHEX()
|
static |
Definition at line 1116 of file Engineering.php.
References $out, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\COMPATIBILITY_GNUMERIC, PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ BINTOOCT()
|
static |
Definition at line 1170 of file Engineering.php.
References $out, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\COMPATIBILITY_GNUMERIC, PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ COMPLEX()
|
static |
Definition at line 1640 of file Engineering.php.
References PHPExcel_Calculation_Functions\flattenSingleValue(), and PHPExcel_Calculation_Functions\VALUE().
Referenced by IMEXP(), IMLN(), IMPOWER(), IMPRODUCT(), IMSIN(), IMSQRT(), IMSUB(), and IMSUM().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ CONVERTUOM()
|
static |
CONVERTUOM.
Converts a number from one measurement system to another. For example, CONVERT can translate a table of distances in miles to a table of distances in kilometers.
Excel Function: CONVERT(value,fromUOM,toUOM)
- Parameters
-
float $value The value in fromUOM to convert. string $fromUOM The units for value. string $toUOM The units for the result.
- Returns
- float
Definition at line 2421 of file Engineering.php.
References PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NA(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ DECTOBIN()
|
static |
Definition at line 1228 of file Engineering.php.
References $out, $r, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ DECTOHEX()
|
static |
Definition at line 1284 of file Engineering.php.
References $out, $r, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ DECTOOCT()
|
static |
Definition at line 1338 of file Engineering.php.
References $out, $r, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\COMPATIBILITY_OPENOFFICE, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\getCompatibilityMode(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ DELTA()
|
static |
DELTA.
Tests whether two values are equal. Returns 1 if number1 = number2; returns 0 otherwise. Use this function to filter a set of values. For example, by summing several DELTA functions you calculate the count of equal pairs. This function is also known as the Kronecker Delta function.
Excel Function: DELTA(a[,b])
- Parameters
-
float $a The first number. float $b The second number. If omitted, b is assumed to be zero.
- Returns
- int
Definition at line 2192 of file Engineering.php.
References PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ ERF()
|
static |
ERF.
Returns the error function integrated between the lower and upper bound arguments.
Note: In Excel 2007 or earlier, if you input a negative value for the upper or lower bound arguments, the function would return a #NUM! error. However, in Excel 2010, the function algorithm was improved, so that it can now calculate the function for both positive and negative ranges. PHPExcel follows Excel 2010 behaviour, and accepts nagative arguments.
Excel Function: ERF(lower[,upper])
- Parameters
-
float $lower lower bound for integrating ERF float $upper upper bound for integrating ERF. If omitted, ERF integrates between zero and lower_limit
- Returns
- float
Definition at line 2268 of file Engineering.php.
References _erfVal(), PHPExcel_Calculation_Functions\flattenSingleValue(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ ERFC()
|
static |
ERFC.
Returns the complementary ERF function integrated between x and infinity
Note: In Excel 2007 or earlier, if you input a negative value for the lower bound argument, the function would return a #NUM! error. However, in Excel 2010, the function algorithm was improved, so that it can now calculate the function for both positive and negative x values. PHPExcel follows Excel 2010 behaviour, and accepts nagative arguments.
Excel Function: ERFC(x)
- Parameters
-
float $x The lower bound for integrating ERFC
- Returns
- float
Definition at line 2332 of file Engineering.php.
References $x, _erfcVal(), PHPExcel_Calculation_Functions\flattenSingleValue(), and PHPExcel_Calculation_Functions\VALUE().
Referenced by _erfcVal().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ GESTEP()
|
static |
GESTEP.
Excel Function: GESTEP(number[,step])
Returns 1 if number >= step; returns 0 (zero) otherwise Use this function to filter a set of values. For example, by summing several GESTEP functions you calculate the count of values that exceed a threshold.
- Parameters
-
float $number The value to test against step. float $step The threshold value. If you omit a value for step, GESTEP uses zero.
- Returns
- int
Definition at line 2215 of file Engineering.php.
References $step, and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ getConversionGroups()
|
static |
getConversionGroups Returns a list of the different conversion groups for UOM conversions
- Returns
- array
Definition at line 2348 of file Engineering.php.
Referenced by EngineeringTest\testGetConversionGroups().
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ getConversionGroupUnitDetails()
|
static |
getConversionGroupUnitDetails
- Parameters
-
string $group The group whose units of measure you want to retrieve
- Returns
- array
Definition at line 2381 of file Engineering.php.
Referenced by EngineeringTest\testGetConversionGroupUnitDetails().
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ getConversionGroupUnits()
|
static |
getConversionGroupUnits Returns an array of units of measure, for a specified conversion group, or for all groups
- Parameters
-
string $group The group whose units of measure you want to retrieve
- Returns
- array
Definition at line 2364 of file Engineering.php.
Referenced by EngineeringTest\testGetConversionGroupUnits().
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ getConversionMultipliers()
|
static |
getConversionMultipliers Returns an array of the Multiplier prefixes that can be used with Units of Measure in CONVERTUOM()
- Returns
- array of mixed
Definition at line 2400 of file Engineering.php.
References $_conversionMultipliers.
Referenced by EngineeringTest\testGetConversionMultipliers().
 Here is the caller graph for this function:
Here is the caller graph for this function:◆ HEXTOBIN()
|
static |
Definition at line 1395 of file Engineering.php.
References $out, $x, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ HEXTODEC()
|
static |
Definition at line 1431 of file Engineering.php.
References $out, $x, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ HEXTOOCT()
|
static |
Definition at line 1477 of file Engineering.php.
References $out, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMABS()
|
static |
IMABS.
Returns the absolute value (modulus) of a complex number in x + yi or x + yj text format.
Excel Function: IMABS(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the absolute value.
- Returns
- float
Definition at line 1729 of file Engineering.php.
References _parseComplex(), and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMAGINARY()
|
static |
Definition at line 1689 of file Engineering.php.
References _parseComplex(), and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMARGUMENT()
|
static |
IMARGUMENT.
Returns the argument theta of a complex number, i.e. the angle in radians from the real axis to the representation of the number in polar coordinates.
Excel Function: IMARGUMENT(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the argument theta.
- Returns
- float
Definition at line 1750 of file Engineering.php.
References _parseComplex(), and PHPExcel_Calculation_Functions\flattenSingleValue().
Referenced by IMLN(), IMPOWER(), and IMSQRT().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ IMCONJUGATE()
|
static |
IMCONJUGATE.
Returns the complex conjugate of a complex number in x + yi or x + yj text format.
Excel Function: IMCONJUGATE(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the conjugate.
- Returns
- string
Definition at line 1784 of file Engineering.php.
References _cleanComplex(), _parseComplex(), and PHPExcel_Calculation_Functions\flattenSingleValue().
Referenced by IMCOS().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ IMCOS()
|
static |
IMCOS.
Returns the cosine of a complex number in x + yi or x + yj text format.
Excel Function: IMCOS(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the cosine.
- Returns
- string|float
Definition at line 1812 of file Engineering.php.
References _parseComplex(), PHPExcel_Calculation_Functions\flattenSingleValue(), and IMCONJUGATE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMDIV()
|
static |
IMDIV.
Returns the quotient of two complex numbers in x + yi or x + yj text format.
Excel Function: IMDIV(complexDividend,complexDivisor)
- Parameters
-
string $complexDividend The complex numerator or dividend. string $complexDivisor The complex denominator or divisor.
- Returns
- string
Definition at line 2040 of file Engineering.php.
References $r, _cleanComplex(), _parseComplex(), PHPExcel_Calculation_Functions\flattenSingleValue(), and PHPExcel_Calculation_Functions\NaN().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMEXP()
|
static |
IMEXP.
Returns the exponential of a complex number in x + yi or x + yj text format.
Excel Function: IMEXP(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the exponential.
- Returns
- string
Definition at line 1972 of file Engineering.php.
References _parseComplex(), COMPLEX(), and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMLN()
|
static |
IMLN.
Returns the natural logarithm of a complex number in x + yi or x + yj text format.
Excel Function: IMLN(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the natural logarithm.
- Returns
- string
Definition at line 1889 of file Engineering.php.
References $t, _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenSingleValue(), IMARGUMENT(), and PHPExcel_Calculation_Functions\NaN().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMLOG10()
|
static |
IMLOG10.
Returns the common logarithm (base 10) of a complex number in x + yi or x + yj text format.
Excel Function: IMLOG10(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the common logarithm.
- Returns
- string
Definition at line 1920 of file Engineering.php.
References _parseComplex(), EULER, PHPExcel_Calculation_Functions\flattenSingleValue(), IMPRODUCT(), and PHPExcel_Calculation_Functions\NaN().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMLOG2()
|
static |
IMLOG2.
Returns the base-2 logarithm of a complex number in x + yi or x + yj text format.
Excel Function: IMLOG2(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the base-2 logarithm.
- Returns
- string
Definition at line 1946 of file Engineering.php.
References _parseComplex(), EULER, PHPExcel_Calculation_Functions\flattenSingleValue(), IMPRODUCT(), and PHPExcel_Calculation_Functions\NaN().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMPOWER()
|
static |
IMPOWER.
Returns a complex number in x + yi or x + yj text format raised to a power.
Excel Function: IMPOWER(complexNumber,realNumber)
- Parameters
-
string $complexNumber The complex number you want to raise to a power. float $realNumber The power to which you want to raise the complex number.
- Returns
- string
Definition at line 2005 of file Engineering.php.
References $r, _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenSingleValue(), IMARGUMENT(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMPRODUCT()
|
static |
IMPRODUCT.
Returns the product of two or more complex numbers in x + yi or x + yj text format.
Excel Function: IMPRODUCT(complexNumber[,complexNumber[,...]])
- Parameters
-
string $complexNumber,... Series of complex numbers to multiply
- Returns
- string
Definition at line 2152 of file Engineering.php.
References _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenArray(), and PHPExcel_Calculation_Functions\NaN().
Referenced by IMLOG10(), and IMLOG2().
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:◆ IMREAL()
|
static |
Definition at line 1710 of file Engineering.php.
References _parseComplex(), and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMSIN()
|
static |
IMSIN.
Returns the sine of a complex number in x + yi or x + yj text format.
Excel Function: IMSIN(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the sine.
- Returns
- string|float
Definition at line 1836 of file Engineering.php.
References _parseComplex(), COMPLEX(), and PHPExcel_Calculation_Functions\flattenSingleValue().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMSQRT()
|
static |
IMSQRT.
Returns the square root of a complex number in x + yi or x + yj text format.
Excel Function: IMSQRT(complexNumber)
- Parameters
-
string $complexNumber The complex number for which you want the square root.
- Returns
- string
Definition at line 1860 of file Engineering.php.
References $r, _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenSingleValue(), and IMARGUMENT().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMSUB()
|
static |
IMSUB.
Returns the difference of two complex numbers in x + yi or x + yj text format.
Excel Function: IMSUB(complexNumber1,complexNumber2)
- Parameters
-
string $complexNumber1 The complex number from which to subtract complexNumber2. string $complexNumber2 The complex number to subtract from complexNumber1.
- Returns
- string
Definition at line 2084 of file Engineering.php.
References _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenSingleValue(), and PHPExcel_Calculation_Functions\NaN().
 Here is the call graph for this function:
Here is the call graph for this function:◆ IMSUM()
|
static |
IMSUM.
Returns the sum of two or more complex numbers in x + yi or x + yj text format.
Excel Function: IMSUM(complexNumber[,complexNumber[,...]])
- Parameters
-
string $complexNumber,... Series of complex numbers to add
- Returns
- string
Definition at line 2116 of file Engineering.php.
References _parseComplex(), COMPLEX(), PHPExcel_Calculation_Functions\flattenArray(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ OCTTOBIN()
|
static |
Definition at line 1528 of file Engineering.php.
References $out, $r, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ OCTTODEC()
|
static |
Definition at line 1564 of file Engineering.php.
References $out, $x, PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:◆ OCTTOHEX()
|
static |
Definition at line 1607 of file Engineering.php.
References $out, $x, _nbrConversionFormat(), PHPExcel_Calculation_Functions\flattenSingleValue(), PHPExcel_Calculation_Functions\NaN(), and PHPExcel_Calculation_Functions\VALUE().
 Here is the call graph for this function:
Here is the call graph for this function:Field Documentation
◆ $_conversionMultipliers
|
staticprivate |
Definition at line 127 of file Engineering.php.
Referenced by getConversionMultipliers().
◆ $_conversionUnits
|
staticprivate |
Definition at line 57 of file Engineering.php.
◆ $_one_sqrtpi
|
staticprivate |
Definition at line 2287 of file Engineering.php.
◆ $_two_sqrtpi
|
staticprivate |
Definition at line 2226 of file Engineering.php.
◆ $_unitConversions
|
staticprivate |
Definition at line 154 of file Engineering.php.
The documentation for this class was generated from the following file:
- libs/composer/vendor/phpoffice/phpexcel/Classes/PHPExcel/Calculation/Engineering.php